This post is a solution to an exercise problem in the book Numerical Linear Algebra by Trefethen and Bau. I am using this book for self-study. I always try to solve the problems after each chapter, but often end up referring to the solutions already published online. I find them very helpful. These problems (10.4.b and c) were not included in the solutions, so this blog is trying to bridge that little gap. Disclaimer, this is just my best attempt, no guarantees of accuracy. Do let me know if you spot mistakes!
Problems:
b) Describe an algorithm for QR factorization that is analogous to Algorithm 10.1 but based on Givens rotations instead of Householder reflections.
c) Show that your algorithm involves six flops per entry operated on rather than four, so that the asymptotic operation count is 50% greater than (10.9)
Solutions:
b) Givens rotation is a rotation in a plane spanned by two coordinate axes. In the problem, a \(2 \times 2\) example matrix is given for a Givens rotation of a 2-D vector.
\[\begin{eqnarray}J(\theta)=\begin{bmatrix}c&s\\-s&c\end{bmatrix},\; c=cos(\theta),\; s=sin(\theta)\end{eqnarray}\]Analogous, general Givens rotation for rotating an \(n\)-dimensional vector is:
\[\begin{eqnarray}G(i,j,\theta)=\begin{bmatrix}1 & \cdots & 0 & \cdots & 0 & \cdots & 0\\\ \vdots & \ddots & \vdots & & \vdots & & \vdots \\\ 0 & \cdots & c & \cdots & s & \cdots & 0 \\\ \vdots & & \vdots & \ddots & \vdots & & \vdots \\\ 0 & \cdots & -s & \cdots & c & \cdots & 0 \\\ \vdots & & \vdots & & \vdots & \ddots & \vdots \\\ 0 & \cdots & 0 & \cdots & 0 & \cdots & 1\end{bmatrix} \end{eqnarray}\]where \(c=cos(\theta)\) and \(s=sin(\theta)\) appear at the intersections of $i$th and \(j\)th rows and columns.
Algorithm 10.1 is Householder triangularization. It consists of by mutliplying matrix \(A_{mxn}\) with a matrix called Householder reflector at each step until \(A\) is converted into a triangular matrix. There are a total of \(n-1\) step. The goal of each step is to introduce more zeros into the matrix until a triangular matrix is obtained. For detailed explanation on triangularizing by introducing zeros, reader is referred to Numerical Linear Algebra by Trefethen, page 70.
Using Givens rotations we can obtain the same kind of step by step triangularization of the matrix \(A\) with dimensions \(mxn\). At each step \(i\) of the triangularization we want to introduce all the necessary zeros in the column \(i\) of matrix \(A\) for it to become triangular. In other words, in each step we apply a transformation to the matrix \(A\) that will set the entries in column \(i\) with row indices \(i+1\) to \(m\) to \(0\).
A Givens rotation rotates a vector in a 2-D plane. We can see it as rotating the component of the vector that is in that plane. A single Givens rotation can introduce one \(0\) into a vector it is rotating if the rotation angle is chosen so it closes the gap between the component of the vector in that plane and one of the axes. For an \(n\)-dimensional vector to have only its 1st entry non-zero, we need to perform \(n-1\) Givens rotations. Each of these is performed in a plane spanned by the axis corresponding to the first vector entry and an axis corresponding to one of the non-first vector entries. The angle also must be chosen carefully so that it ends up aligning the vector component to the first axis.
I illustrate this with an example of a 3-D x vector. First, vector is rotated in the plane spanned by axes \(1\) and \(2\). This can be seen as rotating the component of the vector that is in that plane by the angle \(\theta\) between the component and the axis \(1\). The component of the vector in the plane is shown as a blue vector in Figure 1b). The rotated component is shown in green and the resulting vector obtained by rotating \(x\) by \(\theta\) in the said plane is shown in red in Figure 1b). In the next step \(x_{\theta}\) is rotated in the plane spanned by axes \(1\) and \(3\) by the angle \(\gamma\) between \(x_{\theta}\) and axis \(1\). Finally we obtain the vector \(x_{\theta\gamma}\) with the same norm as vector \(x\) parallel with axis \(1\) (Figure 1c)).
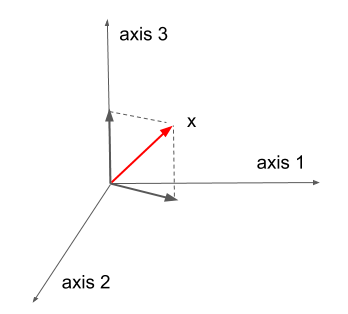 a)
a)
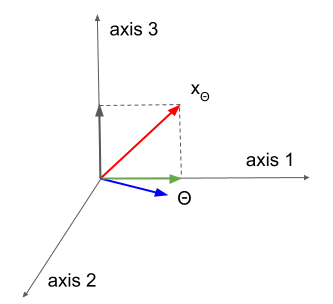 b)
b)
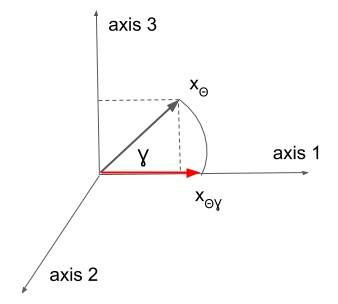 c)
c)
Figure 1.
I have written up the algorithm in Matlab. I give 2 possible implementations. The first one uses Givens rotation matrices explicitly. The second one extracts only the multiplications and sums with non zero matrix elements. The second implementation makes it clear that 6 flops are used per matrix entry as opposed to 4 used by algorithm 10.1. in Numerical Linear Algebra book.
function R = givens1(A)
% Using Givens rotation for matrix triangularization
% Exercise 10.4b) from Numerical Linear Algebra by Trefethen
[m,n] = size(A);
for k=1:n
for j=2:m-k+1
x=A(k:m,k);
h = sqrt(x(1)*x(1)+x(j)*x(j));
c = x(1)/h;
s = x(j)/h;
%This is a way to write the algorithm by explicitly using a Givens rotation
%matrix.
G = eye(m-k+1, m-k+1);
G(1,1) = c;
G(j,j) = c;
G(1,j) = s;
G(j,1) = -s;
A(k:m,k:n) = G*A(k:m,k:n);
end
end
R = A;
end
c) Givens rotation in the plane \(i\) and \(j\) affects only rows \(i\) and \(j\) of the matrix it is applied to. The rows \(i\) and \(j\) of the matrix correspond to the coordinates \(i\) and \(j\) of the vectors made up by matrix columns. We can observe the effect of the rotation on each of the column vectors separately.
A Givens rotation has two non-identity rows each with two non-zero entries. When multiplied with a vector, this comes to 3 operations per each non-zero row: 2 multiplications and a summation. This totals to 6 operations per each column of the matrix rotation is applied to. The below implementation of the triangularization using Givens rotations makes this explicit.
function R = givens2(A)
% Using Givens rotation for matrix triangularization
% Exercise 10.4b) from Numerical Linear Algebra by Trefethen
[m,n] = size(A);
for k=1:n
for j=2:m-k+1
x=A(k:m,k);
h = sqrt(x(1)*x(1)+x(j)*x(j));
c = x(1)/h;
s = x(j)/h;
v1 = A(k,k:n);
vj = A(k+j-1,k:n);
A(k,k:n) = c*v1 + s*vj;
A(k+j-1,k:n) = -s*v1 + c*vj;
end
end
R = A;
end
The inner loop applying the Givens rotations is performed \((m-k)\) times in each step \(k\). Inside the loop, it affects rows 1 and \(j\) of the submatrix of \(A(k:m,k:n)\) it operates on. For each of \((n-k+1)\) entries except the first entry in each of the columns of the submatrix, 6 operations are performed, 4 multiplications and 2 additions. Different entries are operated on in a different pass of the inner loop, with each Givens rotation affecting the first entry but only one Givens rotation affecting any of the other column vector entries. Hence, this version of triangularization applies 6 flops per matrix entry compared to 4 flops in algorithm 10.1 in Numerical Linear Algebra book.